联系我们
-
格鲁夫机械设备制造有限公司
地址:莲池区焦庄乡阮庄村
手机:133-3122-5020
E-MALI:china@gelufu.com
电话:0312-6784766
传真:0312-6784733

当前位置: 首页 > 新闻中心 > 常见问题 > 正文
韧性减速机理与相关数值模拟
浏览次数:269350 时间:2017-10-25
韧性减速机理与相关数值模拟
上一章讨论了稳态扩展前提下的输气管道动态断裂有限元计算。之所以很多研究把稳态扩展作为前提,并曾在相当长的时间内采用Kalininen估算管道极限裂纹扩展速度的(2-6a)式计算裂纹稳态扩展速度,是因为压输送兴起以来,人们曾长期认为材料的抗力远远不足以抵御压气体逸出引起的裂纹驱动力,裂纹不断被加速驱动,直至扩展速度达到了接近于极限速度的稳态值。这确实符合早期动态脆性断裂的观测结果。
随着冶金技术水平的提,管材的性能发生了较大的变化。与此同时,管线的设计压力也有了大的提。原有的动态脆性断裂几乎不再发生。新的动态延性断裂乃至压韧性断裂能够导致断裂速度接近于极限,并形成稳态扩展吗?这个稳态扩展的前提值得怀疑。 3.1从韧性变化看钢制管道动态断裂 在天然气管线裂纹止裂研究的历史上,对管线断裂现象认识有一个提的过程。在管线建设的早期,由于当时冶金水平的局限,管材的韧性水平较低,韧脆转化温度DBTT(Ductile-to-Brittle Transition Temperature)较,发生了很多管线的脆性断裂事故。防止脆性断裂的发生是人们的主要研究课题。管线的工作温度在管线钢的DBTT以下时,动态断裂呈现宏观脆性断裂的特征,即其横纵向断口都为平直的只有很少剪切唇或没有剪切唇的脆性断口。这种动态脆性断裂(DBF)沿着管道的对称面发展,如图3-1a所示。
 为了防止管线脆性断裂事故的发生,人们进行了大量的研究工作,提出了用管材的夏比冲击韧性值和落锤撕裂实验(DWTT)的断口形貌转化温度作为判定管线是否发生脆性断裂的依据。
此后铺设的管线采用了DBTT低于管线工作温度的钢材,用压多次加压检测可能会产生的缺陷,老管线的操作条件等多种措施。实践表明,这些措施较为可靠,基本解决了动态脆性断裂的问题。
20世纪70年代以来,随着纯净钢、连铸板坯及低碳微合金化钢板控轧技术的发展,管材的韧性得到飞跃性的提。随后又引入了计算机自动控制技术和多探头的无损探伤技术等,能够保证超压运行的韧性管道得以实现。近年来,超纯净钢的出现为直焊缝管的发展提供了原材料方面更大的支持,加上整体热处理、热张力减径等原用于无缝管轧制的技术引用于直焊缝管生产,其产品向等级、多元化方向发展,其性能己等同或超过无缝管。 在管道用钢韧性性能大幅度上升的背景下,20世纪60年代,延性失稳断裂事故首次在输气管线上出现。动态延性断裂(DDF)在宏观剪切面上扩展,与管道表面呈45度倾斜角,有很大的剪切唇,如图3-lb和图3-1c所示。虽然这种断裂的环境温度于钢材的韧脆转化温度,但由于钢材的韧性相对于强度较低,还是使动态断裂扩展先于显著的塑性应变而发生。
图3-2显示了DBF和DDF的形貌特征。从图中看出动态延性断裂相比于脆性断裂具有速度较低,裂纹扩展途径比较单一,能自行止裂等特点。由于脆性断裂已被广泛遏止,近二十年来,人们把注意力主要集中在延性断裂的起裂扩展和止裂上,对延性断裂的关注远超过对脆性断裂的研究,目前还远未结束。管线钢动态断裂韧性的测定也就成为了人们关注的焦点。 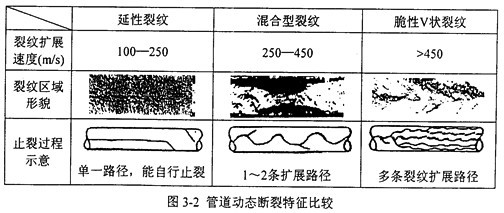 3.2全尺寸实验中出现的减速现象
为了清楚地阐述在韧性输气钢管的全尺寸爆破实验中观测到的由材料韧性引起的裂纹持续减速现象,有必要先对全尺寸实验的方法作较为细致的描述。本节的数据还会用作第四章小试样实验和本章的韧性减速计算的比较。
说到全尺寸实验,就不能不提凭借全尺寸实验数据进行止裂预测的Maxey双曲线法。下面我们就从Maxey双曲线法开始对全尺寸实验中得到的结果以及遇到的问题做归纳性的陈述,同时引出本文的发现和观点。
3.2.1Maxey双曲线方法 在延性断裂的止裂研究中,人们一直试图确定材料的韧性值达到多大,可以使管线具有足够的止裂能力。由于全尺寸实验相当昂贵,且结果仅对应于特定的天然气成分、管道性能等因素,因此需要对实验的特性进行定量化以用于动态延性断裂止裂设计。关于止裂韧性临界值的预判模型, 上应用较多的是1975年BMI的Maxey等人建立的双曲线(Two-Curve)方法。 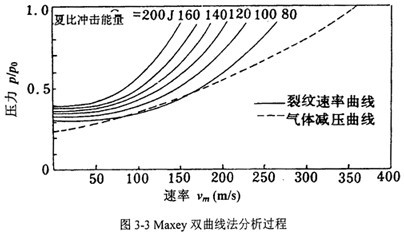 双曲线法的具体分析过程如图3-3所示,坐标横轴表示速度,纵轴表示气体压力或环向应力。上方的一组曲线表征不同韧性水平下的断裂速度,是内压或环向应力的函数。随着内压或环向应力在断裂过程中的减小,断裂速度不断降低。如果压力或应力足够低,断裂速度即减小到零而发生止裂。
下面的虚线与气体减压波速有关,它也是环向应力或管道内压的函数。在减压过程中,连续的减压波沿管子传播,对应于每个压力有一个的波扩展速度。因此在减压波沿管线从开裂源传播时在很宽的速度范围内压力是连续的。
根据管道动态断裂扩展与止裂的减压波速判据,当裂纹扩展速度低于管内介质的减压波速度时,裂纹会停止扩展;当裂纹扩展速度于管内介质的减压波速时,不会发生止裂。
这种说法的依据是:对于前一种情况,从裂源处开始,减压波前沿的移动速度比断裂扩展速度更快,使得裂纹尖端的管壁应力因减压波的通过而不断减小,并 终降至止裂应力水平以下而使裂纹止裂;反之裂纹尖端的压力不发生变化,断裂将持续扩展,因为裂纹尖端的动态袭纹驱动力不会减小。 如果断裂速度曲线和压力波速曲线不相交,则在任何条件下减压波速都大于断裂速度。根据减压波速判据,裂纹扩展将发生止裂。如果两曲线相交或相切,则 少有一点压力所对应的压力波速和断裂速度是相等的。这时管道将发生持续的裂纹扩展。因此,图3-3中两条曲线的切点对应于止裂所需的临界韧性,切点处的横坐标即为稳态扩展情况下的断裂速度。
为了得到数值解答,Maxey的延性断裂模型总结出了裂纹扩展速度和管内压力(或环向应力)之间的经验关系: 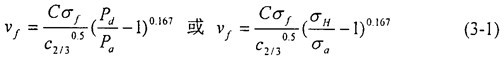 式中vf表示断裂扩展速度(m/s);C是由经验确定的回填常数;σf为流动应力,MPa,σf =(σy+σu)/2,σy为屈服应力,σu为拉伸强度:c2/3为2/3厚度试样的夏比冲击韧性值(J/mm2);Pd为裂尖处的气体压力(MPa);Pa为止裂时的气体压力(MPa);σH为裂尖处的环向应力(MPa);σa为止裂时的环向应力(MPa)。
式(3-l)中止裂压力(环向应力)Pa(σa)有如下的计算关系式:
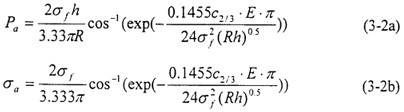 式中R为管道半径(mm);E为弹性模量(MPa);h为管道壁厚(mm)。
这种双曲线法的处理还被用于处理富气输送问题。乙烷等其它烷类气体的混入引起了两相减压行为。在两相状态下,减压波速曲线会在相变过程区产生平台,表明相变阻碍了气体从开裂的管道中逸出,使得裂纹止裂更加困难。
在双曲线法的基础上,结合大量的实验结果对止裂韧性进行标定,世界各大研究机构分别给出了简便易算的经验公式用以估算临界止裂韧性,列举如下:
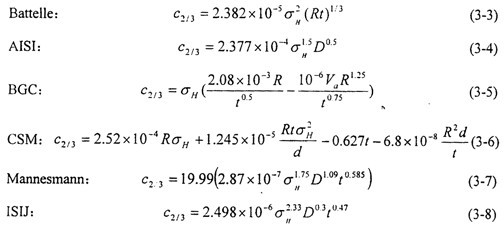 其中c2/3为估算的2/3尺寸单位面积夏比冲击临界止裂韧性(J/mm2);d为埋入深度(mm);其余符号的物理意义与单位与前面相同。
Maxey双曲线法及导出的经验公式的优点在于理论及算法比较简单,易于工程应用,因而从20世纪70年代起被 上广泛采纳,并通过了实验的检验。 必须指出的是,这些经验公式都是根据早期的低韧性全尺寸实验(CVN能量小于100J)数据经常数标定而得出的,对于韧性管线钢,这些公式出现了明显的偏差。随着近年来管道钢管材料特性的变化,材料强度及韧性的提,以及压富气输送工艺的采用使已有的止裂预测公式偏于危险。
图3-4表示了Battelle应用Maxey双曲线法对全尺寸实验数据库所做的DDF止裂韧性预测,图3-4a至图3-4f分别对应于式(3-3)至式(3-8)。图中显示的实验用管的钢级包括X52到Xl00,管径范围从4O6mm到1422mm,实验 压力超过16MPa。可见,预测模型在管材韧性低于某一水平时预测结果与实物实验结果基本吻合,但当管材韧性较时出现明显偏差,预测应该止裂的管线没有止裂。经典的止裂预测模型在预测夏比能量值于94J的管材时,已经偏于危险,即过估计了管材的止裂性能。
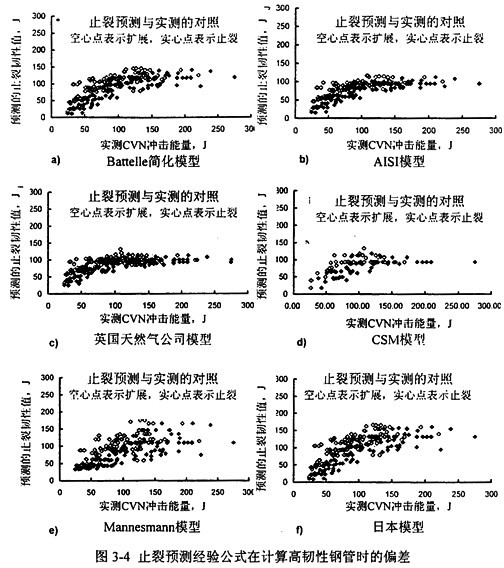 为了保留原有的经验算法,1997年Leis认为保证该算法准确的临界韧性值为94J,并对韧性结果做了修正:
预测冲击韧性CVN>94J时:CVN′=CVN+O.002CCVN2.04-21.18 (3-9) 预测止裂冲击韧性CVN<-94J时因非线性影响不明显而不做修正。
这种修正方法仅是一定范围内根据真实实验结果的近似归纳,并不能从趋势上解决双曲线法在描述韧性淬火回火钢时出现的偏差。其原因是韧性钢出现后,传统的动态实验手段引起与断裂无关的显著能量散失。
3.2.2全尺寸爆破实验(Full-Scale Burst Test)简介
全尺寸实验的费用昂贵,周期长。实验过程中要求系统地变化压力、管径、壁厚、强度以及韧性等变量,因此实验操作难度大,重复次数多。做过水压爆破实验,压输气管道实验尚无先例。目前已知的实验数据来源有意大利CSM的钢制管道实验、美国西南研究院的PE管道实验、加拿大一美国联盟管道实验和日本HLP组织实验。 全尺寸爆破实验一般设有一根有预制裂纹的低韧性钢管在管段中部作为起裂管,两侧焊接钢管的韧性沿裂纹扩展方向递增排列。裂纹从起裂管向两侧扩展,停止扩展部位的钢管韧性就是设定运行条件下的管线止裂所需的韧性。断裂扩展速率在低韧性的起裂管开裂后测量。 全尺寸实验使用甲烷、空气或者氦气作为压力介质。实验分为地上管线和埋地管线两种。由于按照原来的止裂预测方法己经不能保证现代强度韧性管线的延性断裂止裂性能,20世纪80年代美国天然气协会AGA委托包括美国SwRI和意大利CSM在内的多家机构进行了合作研究,试图得到一种理论上可靠,实验证明可行的防止管线延性断裂长程扩展的方法。 欧洲管线研究组织EPRG也在20世纪70年代进行的实物实验的基础上从1983年开始对韧性的管线钢管进行了大量的实物实验,并于1995年公布了强度管线钢止裂韧性推荐值,1996年制定的1502183-3管线钢管技术条件采用了EPRG的推荐值。1985年日本几大钢铁公司联合进行了一次较大规模的实物实验,基于Maxey的双曲线法对实验结果进行了分析,得到了有价值的结论。 下面结合两次大规模全尺寸实验宝贵的完整数据对全尺寸实验测试情况进行说明,其中真实断裂速度与CVN韧性止裂预测是本文重点关注的对象。
3.2.1.1北美联盟管道全尺寸爆破实验
北美联盟管道总投资30亿美元,由6家公司合资兴建,全长2627km,从加拿大的British Columbia到美国的Illinois,计划2000年投入运营。该管道设计输送能力为每天375×105m3,主干线设计 大输送压力为12MPa,管径9l4mm;支线管径1067mm, 大设计压力为8.274MPa。 联盟管道的设计在几个方面都创造了新的世界水平: 韧性管线钢管——CVN冲击韧性于217J; 的操作压力—— 大操作压力12MPa;
富气输送——含15%乙烷,3%丙烷,天然气 大热值为44.2MJ/m3。 为了验证联盟管道Φ914和Φ1067钢管的止裂韧性,进行了两组全尺寸瀑破实验,实验管段全长约366m,中间为9根11m长的实验样管,爆破实验时裂纹将在其中进行扩展。实验样管沿东西方向分别标为1E、2E以及1W、2W等,预制裂纹穿过1E和1W之间的环焊缝。第一次实验的示意图如图3-5所示。
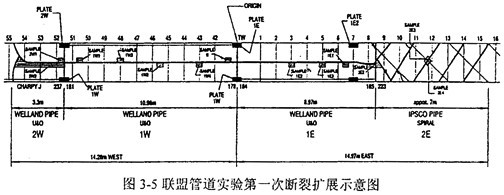 表3-l给出了各实验管段的夏比冲击功以及按照实验工况用Maxey双曲线法预测的止裂韧性数值。
表3-l联盟管道爆破实验夏比冲击能量数值(单位:J)
第一次爆破实验采用Φ914钢管,壁厚14.2mm,钢级X70,操作压力12MPa,实验温度23.8℃,天然气热值为44.6MJ/m3。
通过炸药爆破法,裂纹穿过1E和1W中间环裂缝,并在钢管顶端开始扩展。第一次爆破实验中实验断口均为韧性断裂,在样管1W中,裂纹沿轴向直线扩展,在样管1E中,裂纹沿轴向直线扩展将近钢管末端时,其扩展方向稍有倾斜,但在1W和1E中均未发生止裂。在1W样管的末端,裂纹穿过环焊缝直接进入2W样管中继续直线扩展约2m后转向并绕钢管环向扩展一圈后止裂,环向的一圈裂纹将实验管线分割成东西两部分。在1E样管的东端,在距离1E、2E环焊缝0.5m的地方,裂纹由轴向直线扩展转化为撕裂型剪断扩展,随后扩展进入2E样管(螺旋缝焊管)中,呈螺旋线沿2E样管向前扩展,裂纹扩展方向垂直于样管的螺旋焊缝,在裂纹螺旋状前进约4.25圈后止裂。 第二次爆破实验是为了模拟Φ1067钢管的止裂过程,由于实验设备不到位, 终仍采用功914钢管,壁厚14.2mm,钢级X70,操作压力12MPa,实验温度16.5℃。通过双曲线法判定止裂韧性与试图模拟的钢管相同。 实验二的断口均为剪切断裂,裂纹扩展长度为33.6m。由于1W和1E冲击功低于预测的止裂冲击韧性,因而裂纹均沿1W和lE轴向直线扩展并分别进入2W和2E样管, 后在2W和2E样管中止裂,如图3-6所示。 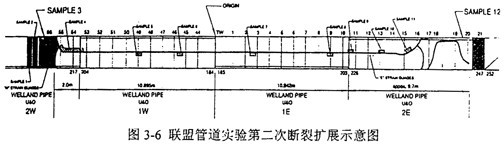 在2E样管中,裂纹直线扩展约4.5m后开始转弯沿螺旋线扩展。当遇到直焊缝后又产生一个二次裂纹,二次裂纹沿直焊缝扩展约1m后也开始转向沿螺旋线扩展。当主裂纹第二次遇到直焊缝时,先沿直焊缝扩展lm多长然后转向扩展并随即止裂。
断裂扩展全程将压力传感器采集的压力数据与上述断裂扩展速度绘制成压力一速度曲线,根据Maxey双曲线法做出了止裂韧性的预测。在考虑Leis修正(3-9式)的基础上,该预测与实验结果吻合良好。 3.2.1.2日本HLP组织实验 1978年,日本钢铁学会(ISIJ)成立了强度输送管HLP(High-strength Line Pipe)专业研究委员会。该组织在1978-1983年间进行了七次全尺寸爆破实验,其中五次在Kamaishi(釜石,编号A1、A2、A3、Bl、B2),两次在BGC(英国天然气公司,British Gas CoMPany,编号Cl、C2)。 实验材料是经控轧(Controlled-Rolled)或调质(Quenched and Tempered)工艺制造的APIX70管,直径1219mm,壁厚18.3mm。A和B系列实验采用空气作为压缩气体,实验温度在3℃到12℃之间。C系列实验采用天然气(富气),实验温度为-5℃。实验用管道气压除C2外均为11.6MPa,C2采用10.4MPa。 每段钢管长约10m,每组实验采用7段管材环缝焊接,并在每端焊上壁厚为26.67mm的蓄气管,全长约150m。实验管段置于地下l.3m深处,除蓄气管外的部分回填上砂子。实验外观形貌如图3-7所示。
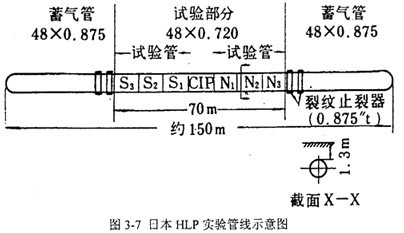 裂纹的爆破源是一条500mm长沿轴向切割的穿透裂纹,设置在裂纹起始管CIP(Crack Initial Pipe)的中心,两侧管段按南北方向分别标号为S3、S2、S1和Nl、NZ、N3。在裂纹扩展期间,测量了裂纹扩展速率、压力降低和应变变化。
实验采用了大量不同韧性的钢管,按照一定的顺序排列。
A系列实验中,裂纹沿夏比冲击能量CKV值约为50J的起裂管CIP,依次穿过韧性值递增排列的钢管。各管段的大致韧性值是在每次爆破实验后经过精心研究确定的。A3中Sl到S2是的例外; B系列实验中,起裂管两侧同一方向的管段韧性值大致相同,是为了研究两根全长范围内具有相同价F值的管子的裂纹扩展行为,两侧夏比冲击功预设为120J和150J。另外,B系列实验中起裂管CIP的韧性较(CKV约90J),长度较长(约16m),以减轻起裂过程对实验段的影响; 在C系列实验中,因压缩气体为多种成份的天然气,在开裂减压时将引起相变,阻碍了气体的逸出,使止裂变得困难,因而普遍选用了韧性钢管。 管道排列顺序和各段对应的夏比冲击功价;CKV、DWTT功DS和预开裂DWTT功DP如表3-2所示。
表3-2日本HLP管道爆破实验各段CVN与DWTT吸收功(单位:J)
在全部七次HLP实验中,裂纹扩展与止裂的情况如图3-8所示。
在图3-8的所有实验中,裂纹以全延性方式向实验管两端呈轴向扩展,并突然转向周向,随即止裂。这表明管道本身的韧性导致止裂。
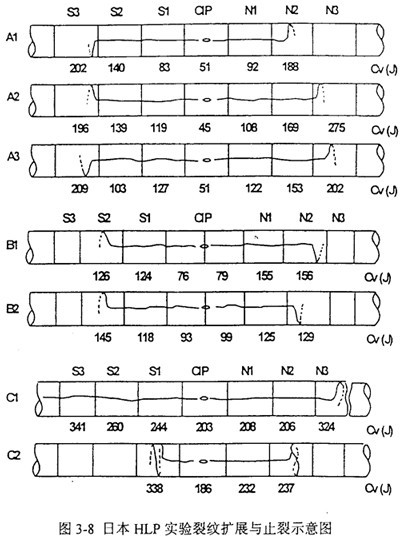 3.2.3速度观测结果
在全尺寸爆破实验中,可以根据时线记录的数据计算裂纹沿钢管轴向的扩展速度。图3-9和3-10分别在联盟管道第一次和第二次实验的断裂速度曲线。
从图中可以看到,在裂纹长度不超过三倍管道直径的超始扩展阶段,因钢管内的气压来不及释放而裂纹加速较快;
在裂纹扩展长度相当于第四个管道直径长度的范围内,钢管裂口张开,气体压力迅速衰减,直至与裂纹扩展速度达到平衡,此阶段断裂速度先升后降;
随着裂纹的进一步扩展,扩展过程的参数包括裂纹扩展速度以及裂纹尖端的应力取决于钢管的断裂韧性。
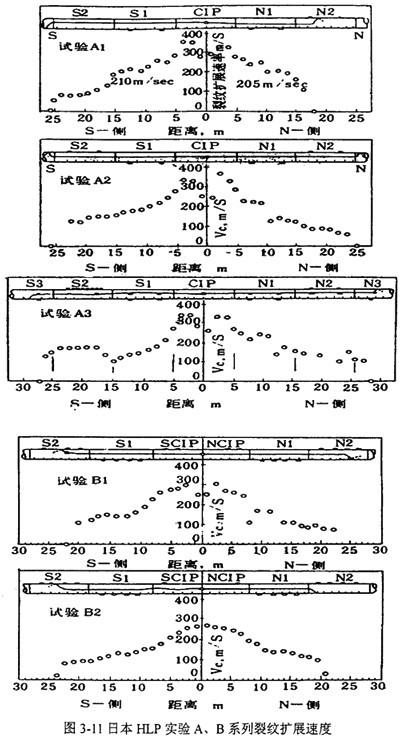
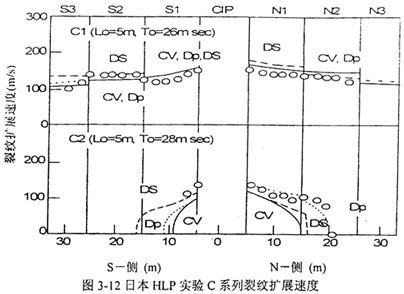
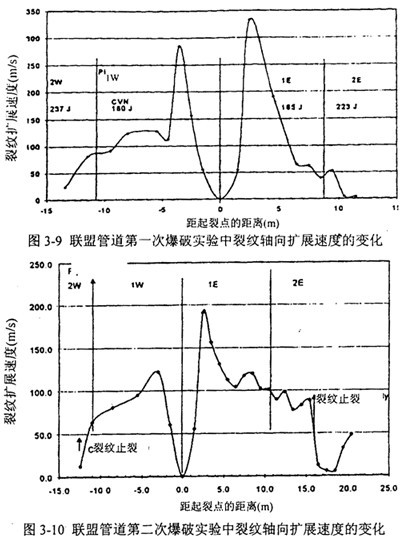 图3-11、图3-12表示日本HLP实验中裂纹扩展速率随扩展距离的变化,空心点为实测值。通过对易发生断口分离(断口分离现象将在下一章中介绍)的控轧(CR)钢和调质(QT)钢两种材料的临界止裂韧性的测试,没有发现大的差异,说明断口分离现象对动态延性断裂的止裂能力影响不大。
速度曲线表明,在A类实验中,裂纹起裂后,在韧性较低的CIP扩展速度达以300m/s以上。裂纹进入实验管后,裂纹扩展速度随着裂纹的扩展而下降,实验A3的南侧有例外,裂纹从S1到S2管裂纹扩展速度增大,这是由于韧性排列时S2管的韧性例外地比S1低。在B类实验中,CIP管的 大裂纹扩展速度率为300m/s(B1)和270m/s(B2),这与其韧性较有关。
  3.2.4从全尺寸实验中得到的结论
本节介绍了现有的基于全尺寸实验的止裂韧性判定方法,搜集整理了 上两次著名的大规模钢制输气管道全尺寸实验的进行情况和各管段材料性能以及实测裂纹扩展速度数据。以下几点与论文密切相关: 首先,管道断裂动力学上的有限元法是近十几年随计算机的发展而蓬勃兴起的技术,其精确程度与具体设计参数下的可靠性还有待在进一步的实践中证实。在此背景下, 上已经沿用了近三十年的全尺寸实验确定管道止裂韧性的方法无疑为计算提供了很好的原始数据与结果比较; 其次,我国目前尚没有进行压输气管道的全尺寸爆破实验,的实验我们可以得到的数据十分有限,因而显得弥足珍贵。具体的实测数据,只有和实验条件,设计参数,各段钢材性能等参数结合起来才有参考价值; 后,也是 重要的一点,双曲线法在结合全尺寸实验在预测韧性管道止裂韧性时已发生巨大的偏差,如图3-4所述。究其原因,本文认为很大程度上是由于韧性钢材的明显的塑性功耗散现象己经使全尺寸实验的结果背离了双曲线法止裂分析的初衷。这正是本章计算试图解决的问题。 对于 后一点,具体解释如下:
传统分析气体爆破实验的方法是将实验管分成两组,即“扩展组”和“止裂组”,它们取决于裂纹顺利通过管道还是在管道内止裂,然后在两者之间求出冲击韧性临界值。这种做法的正确性是建立在动态裂纹扩展速率在同一韧性的钢管中基本不变,且不会明显受到管道接头部位的影响的前提下的。但现有的韧性管道实验数据表明,在韧性一致的管段中,也会发生断裂扩展速度逐渐减慢直至止裂的现象。对于韧性钢管,这种效应尤其明显。这一结论可以从上两节的实验数据中得到证实,例如:
所有实验的止裂都不是在同一管段内部发生的,任意管段内均发生了减速。尤其是HLP组织的B类实验:在Bl的两侧,B2的北侧,裂纹从CIP起裂后经过的两段管子韧性相差无几,却均在第一段中持续扩展而在第二段中止裂。 这说明止裂与否不仅取决于管段的韧性,还取决于裂纹进入管段的速度,以及裂纹在管段内扩展的距离。也就是说,对于断裂韧性于一定数值的管道,只要长度足够,就必然会发生止裂。因而,对应于某种韧性,仅有是否止裂的结论是不够的,止裂长度概念的引入十分必要。
从本节的讨论看出,韧性管线中裂纹止裂韧性的临界值取决于要求的止裂长度。这需要建立新的能够考虑到止裂长度影响的模型。对于动态裂纹扩展的有限元算法,要考虑韧性导致的减速行为,应将实验可测的韧性作为参数代入,在数值模拟中起到减速的作用。 3.3实测减速模型 通过上一节对全尺寸实验中减速现象的描述,很容易想到的解决方法是直接利用实测速度曲线,对具体应用的管道裂纹扩展速度规律做参数拟合,进而进行有限元计算。实测减速模式正是基于这种思路。
3.3.1实测减速模型的描述 一般地,对管线裂纹扩展速度变化,采用(3-10)式进行拟合:
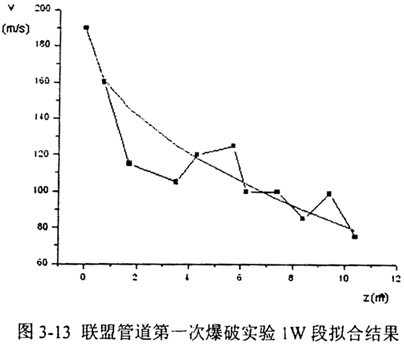
 式中助是拟合段曲线的初速度,Lr表示该初速度下的止裂长度,z表示裂尖位置。对于图3-9中的lW段,取v0=200m/s,Lr=35m,拟合结果如图3-13所示:
 考虑到影响管道裂纹扩展速度变化的参数主要有管道内部气体压力p0,管道的直径D和管道的壁厚h,和管道动态断裂强度和韧性参数等,可分别定义v0和Lr为:
 其中pa为大气压力,σf为流动应力,等于屈服应力和拉伸强度的平均值;CV为CVN实验测得的夏比冲击功,k1和k2分别是具有长度量纲的常数,由实验归纳得到。
3.3.2实测减速模型的不足 作者曾在(3-10)至(3-12)的基础上,与唐甜合作,对西气东输管线进行了评估。本文的重点不在于此,因而不再重复。 实测减速模型毕竟仅仅基于经验公式,缺乏足够的理论基础。其主要的表达式(3-10)至(3-12)成立的依据还存在一些不确定的因素,k1和k2的数值通过现有的全尺寸实验数据也难以定为常数,只给出大致的量级范围。另外,指定裂纹速度变化的规律之后再判断裂纹是否止裂,不足以单独用作工程上判断管道止裂性能的凭据。 3.4韧性减速机理
本节以裂纹扩展过程中整体及裂纹尖端区域的能量平衡方程为出发点,应用流变断裂学中的基本原理,得到宏观唯象形式的表达,并应用于有限元模型。其中表示材料韧性的关键参数通过后的小试件实验得到,个别关键系数通过全尺寸实验的检验确定。
3.4.1含裂纹的钢制管道能量平衡方程 按照流变断裂学的观点,不可逆的裂纹扩展区别于受绝热或等温变形约束的理想弹性体的重要特征是开裂物体的墒增现象,因而采用包括描述熵增、热膨胀、热传导等过程所需的七个参数来描述裂纹扩展过程。 裂纹体的整体能量平衡意味着动能时间变化率与内能时间变化率的总和等于全部力与力偶的功率及单位时间内流进或流出物体全部其余能量(对于本文问题仅考虑热能)的总和。也就是说,作用于物体上的功增量δW与物体吸收或散逸的热能增量δ 的总和等于物体的内能增量△U与动能增量△K的总和,即: △K+△U=δW+δ 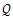 (3-13) (3-13)式中动能和内能均是可加和的状态函数,仅与初始态和终结态有关。但功和热还与过程有关,为此采用了△和δ两种增量记号。
若增量无穷小,且方程中的物理量对于时间是可微函数,则式(3-13)可以写成对时间t的微分形式: 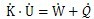 (3-14) (3-14)由于动能和内能是可加和函数,故有:
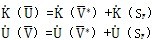 (3-15a) (3-15a) (3-15b)
式中
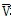 和SF分别为管道所占空间域和裂纹扩展引起的新表面, 是二者之差。若令新裂纹面的能量变化率为: 和SF分别为管道所占空间域和裂纹扩展引起的新表面, 是二者之差。若令新裂纹面的能量变化率为: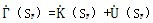 (3-16) (3-16)则可得到:
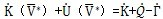 (3-17) (3-17)将上式写成微分形式:
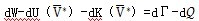 (3-18) (3-18)式(3-18)中,W表示外力功,U表示应变能,K表示动能,Γ表示表面能,
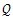 表示热量引起的能量损失。( 表示热量引起的能量损失。( 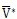 )表示除去裂纹扩展形成的新表面以外的部分的值。 )表示除去裂纹扩展形成的新表面以外的部分的值。下面考虑单侧裂纹扩展的全管道模型,即图2-6中1/4管道模型的两倍。
令Λ=-
 ,表示由于塑性功卸载引起的热耗散量,并将Λ和Γ分别写成塑性功率λ与表面能密度y与裂纹扩展导致新生成表面面积的乘积: ,表示由于塑性功卸载引起的热耗散量,并将Λ和Γ分别写成塑性功率λ与表面能密度y与裂纹扩展导致新生成表面面积的乘积:Λ=2ahλ,Γ=2ahy (3-19) 式中a表示裂纹单向扩展长度,h表示厚度。
定义裂纹单侧扩展的驱动力G:
 一般可设钢材的表面密度y为材料常数,同时注意这里λ与Gd均是与裂纹扩展速率v相关的量。对于瞬态扩展,某时刻的断裂韧性Gd可以表示为:
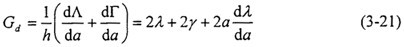 对于金属材料,λ通常比y大三个数量级,故y可忽略不计。
在裂纹扩展的过程中,局部能量不守恒。此时的管道裂纹尖端可视作为一个热源汇,为裂纹的扩展积累和提供能量,并遵循G=Gd的关系。
由(3-14)和(3-21)式, 终得到裂纹单侧扩展的能量平衡方程:
 式(3-22)中da/dt=vt表示t时刻管道裂纹的瞬时扩展速度。
从以上推导可以看出,输入功率dW/dt一定的情况下,热耗散率λ起到了制约动能K的作用。裂纹扩展过程必然伴随有热传导和墒产生,对于耗散型材料(如韧性钢),热耗散效应不容忽视。 3.4.2有限元中的速度反馈机制
首先给出第二章的有限元漠型中时间步长为n时的各能量求解表达式。
外力功表达式为:
W0=0,Wn=Wn-1+
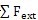 (dn-dn-1) (3-23) (dn-dn-1) (3-23)式中d为节点上的位移分量,
 为作用在节点上的外力。 为作用在节点上的外力。在时间步为n时的动能表达式为:
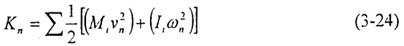 式中i为节点号,M是集中于节点处的质量,I是集中于节点处的转动惯量,vn是节点的线速度分量,ωn是节点的角速度分量。
在时间步为n时的应变能表达式为:  式中h是单元厚度,
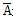 是单元面积,σ和ε是单元的应力和应变。 是单元面积,σ和ε是单元的应力和应变。设时间步为n,迭代步为k,对于任意的变量E ,以△ 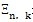 表示 表示 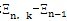 。 。根据上一节所得到的式(3-22),在有限元计算中引入速度反馈机制。注意到(3-23)到3-25)式均为图2-6中1/4管道模型下的值,相当于上一小节中相应物理量的一半,验算下式:
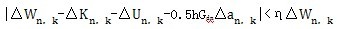 (3-26) (3-26)式中η表示能量平衡迭代要求的精度,0<η<l,越接近于零表示精度越。若(3-26)式成立,则进入n+1时间步计算;若不成立,则进入k+1迭代步:
 以得到的
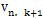 为新的试算速度进行迭代,直至(3-26)式满足。 为新的试算速度进行迭代,直至(3-26)式满足。(3-27)式具有其确切的物理意义,即: 若(l-η)△ 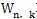 >△ >△ +△ +△ +0.5hGdn△ +0.5hGdn△ ,表示外力功过剩。过剩的部分将通过(3-27)式转化为动能; ,表示外力功过剩。过剩的部分将通过(3-27)式转化为动能; 若(l+η)△
 >△ >△ +△ +△  +0.5hGdn△ +0.5hGdn△  ,则表示外力不足以抵消断裂韧性及应变能变化,这时需要牺牲动能来保证裂纹扩展。 ,则表示外力不足以抵消断裂韧性及应变能变化,这时需要牺牲动能来保证裂纹扩展。在式(3-27)中,以裂尖速率替代了管道整体平均速率反映动能带来的影响。考虑到二者趋势上的一致性,并因等式左端的
 是试算值,仅影响到计算速度与收敛性,而不影响计算精度,故可暂作此假定。 是试算值,仅影响到计算速度与收敛性,而不影响计算精度,故可暂作此假定。速度反馈机制的收敛性同网格疏密程度,时间步长,试算初速度等相关。它在程序中实现的流程如图3-14所示。
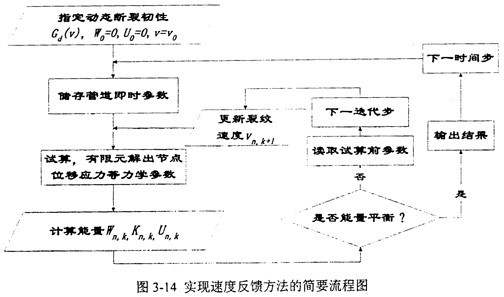 裂纹体的残余动能并不能全部用于驱动裂纹扩展,因为相当一部分动能包含在裂纺顶端后面较远的区域内。Hahn(1973)对双悬臂梁试样的测试表明,约有85%的动能消耗于裂纹驱动能。修正后的(3-27)可以表示为:
 至此,韧性减速机理已经基本建立。但(3-26)式中表示动态断裂韧性的关键量Gd的确定方法尚未解决。下面-小节我们将就此展开讨论。
3.4.3小试样冲击实验与Gd的关系
工程上广泛使用小试件冲击实验的办法测定管道材料的动态断裂韧性,具体测试手段与结果在第四章另有详述。
本小节的目的是通过小试样冲击实验的设计参数和测得的吸收功,给出韧性减速机理中代表动态断裂韧性的关键量Gd的基本表达。 2.1.4节已经提到,动态断裂韧性Gd除与材料的性质密切相关外,还与环境温度,应力状态,试件厚度,特别是断裂速度关系密切。 因小试件冲击实验与管道全尺寸裂纹扩展的相似性,忽略应力状态对断裂韧性的影响。设小试件冲击实验中的特定参数为试件厚度h0,冲击速度v0,实验环境温度T0,韧带宽度即裂纹扩展长度a0,测到的外力吸收功为W0。 由忽略表面能的(3-21)式,小试件裂纹扩展中的动态断裂韧性Gd0。可表示为:
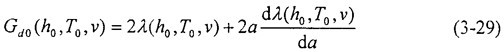 式中λ为材料的塑性功率,v为瞬时扩展速率,a为瞬时裂纹长度,O<a<a0。注意这里裂纹每扩展da,新增裂纹面面积为2hda。
考虑裂纹扩展过程中的某微小时间增量dt,对小试样冲击的实验过程应用能量平衡方程(3-22)式并对裂纹扩展全过程在时间上进行积分: 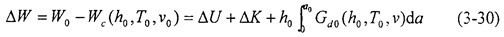 式中△W、△U、△K分别为裂纹扩展过程中试件消耗的外力功、应变能增量和动能增量,WC为裂纹开裂过程消耗的起裂功。对于韧性钢,△U、△K可忽略。
因小试件试样断裂时间很短,可假定起裂后的断裂速度始终等同于摆锤的冲击速度v0。另外考虑在试样尾部因裂纹前端发生塑性形变的范围变短,Gd会相应有所损失,令这-部分损失的能量为P(h0,T0,v0),则:
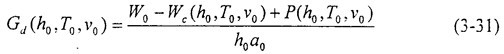 式(3-31)可以作为确定式(3-26)至式(3-28)中Gd(h,T,v)的依据。
3.4.4待定参数的确定
式(3-31 )留下了We和P两个参数有待确定。根据其物理意义,可以通过预制裂纹、脆化缺口等方法消除We的影响。双试件实验更可以达到双重目的,通过两次不同韧带宽度a1和a2的试件(其余条件相同)的实测吸收功W1,W2之差,可以直接得到Gd0: 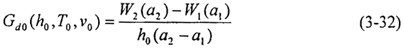 因为影响韧性的参数比较复杂, 可靠的做法是采用和真实管道同样的壁厚,在一系列温度和冲击速度下用双试件法测定断裂韧性,以备计算采用。
3.5基于韧性减速机理的算例分析
韧性减速机理应用于有限元计算后,可以方便地随意指定计算区域内的管道裂纹的初速度v0,通过第四章的小试件方法测到的动态断裂韧性Gd,模拟整个管道包括速度变化的曲线在内的真实开裂情况。
本文通过上述方法,对图3-9至图3-12中的全尺寸实测断裂速度曲线结果进行了校核,得到了比较吻合的结果。现以联盟管道第一次实验IE段为例,设定扩展的初速度为330m/s,速度变化的计算值同实验对比如图3-15所示:  通过大量的测算与归纳,得到吻合较好时的Gd与CVN能量的关系:
Gd=1.3CKV=0.016CKV (3-33)
式中cKV和CKV分别是单位面积夏比冲击韧性值和夏比冲击功,cKV=CKV/(hoao),对于CVN试件,h0=10mm,a0=8mm。
另外,当断裂速度降至低于100m/s时,要考虑偏随速度的降低: 当v<100m/s,Gd=o.8cKV+0.5cKV·v/100 (3-34)
直至止裂时Gd降为止裂韧性0.8cKV。
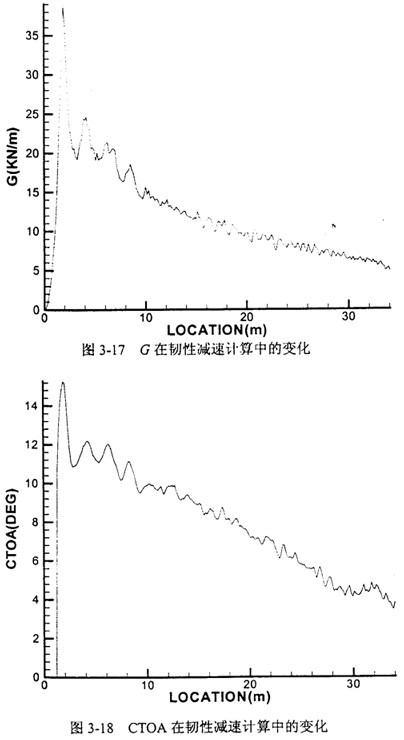
(3-33)和(3-34)式中的系数1.3和O.8的获得方法为大量试算后取与全尺寸速度实测结果普遍吻合较好的值。 根据图3-16中的MISES应力分布可以判断裂尖处的塑性区范围。随着裂纹扩展过程中韧性导致的速度降低,塑性区的范围逐渐缩小。  图3-17和图3-18是针对西气东输某特定设计参数的管线,应用韧性减速机理计算时能量释放率G和裂纹尖端张开角CTOA的变化。
随着计算输入韧性Gd导致的裂纹不断减速,G和CTOA衰减幅度明显,直至止裂。
 3.6本章小结
全尺寸爆破实验中观测到的速度变化表明,对于韧性管线,由塑性功耗散引起的动能衰减不可忽略。裂纹在低于预测断裂韧性的均质管道中也会发生明显的减速现象,直至止裂。Maxey双曲线法在预测韧性钢止裂韧性时发生的偏差是上述论述的有力旁证。
为此我们引入了依靠全尺寸实验指定裂纹扩展速度变化的实测减速模型,将全尺寸实验的速度历史通过参数分析应用到待测管线。因影响裂纹扩展速度的原因过于复杂,这种做法的可靠性不能保证。 本章的主要工作是通过流变断裂学的基本理论,推导了对于瞬态裂纹扩展,动态断裂韧性在整体能量平衡方程中所起的作用,并在有限元中构造了迭代算法。表征材料韧性的参数GJ(v)通过小试样实验确定,在计算中作为已知函数代入。 通过和真实裂纹扩展曲线的对照,建立了通过夏比冲击功估算GJ的经验模型(3-33)和(3-34),并据此对特定参数的管道进行了分析。 夏比冲击和DWTT实验测试的是试样断裂的总能量。总能量包括起裂能、裂纹扩展能、塑性变形能和抛掷试样的动能。已有对DWTT试样的研究认为前两部分能量占总能量的绝大部分。因而,本文认为双试件DWTT实验是 合适的小试件测定Gd(v)的手段。 但对于大多数工程情况,该实验条件难以被满足。这就需要采用判定动态断裂韧性的一般方法,如CVN和DWTT,尤其是CVN。这是因为工程上往往备有各种温度下的一系列夏比冲击能量的数据。 在用全尺寸管道实验的数据作校对的时候,同样会遇到类似的问题。一般情况下关于管道韧性的数据仅有CVN冲击能量和DWTT吸收功,所以有必要对这两种实验进行进一步的分析。有关CVN和DWTT实验方面的内容,尤其是韧性钢材的特性和测试结果,将在下一章中详细讨论。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




 电子营业执照
电子营业执照